目录
一,计数排序
1,基本思想
2,思路实现
3,计数排序的特性总结:
二,排序算法复杂度及稳定性分析
三,排序系列所有源代码
Sort.h
Sort.c
Stack.h
Stack.c
一,计数排序
计数排序也叫非比较排序;
1,基本思想
计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用
操作步骤:
1,统计相同元素出现次数
2,根据统计的结果将序列回收到原来的序列中
图解原理:
对这样一个不需要比较的排序就完成了;
2,思路实现
// 计数排序
void CountSort(int* arr, int n)
{
int i = 0;
int max = arr[0], min = arr[0];
//找最大,最小值
for (i = 0; i < n; i++)
{
if (arr[i] > max)
{
max = arr[i];
}
if (arr[i] < min)
{
min = arr[i];
}
}
//空间大小
int sum = max - min + 1;
//开辟空间并且使元素值都为0
int* arr1 = (int*)calloc(sum, sizeof(int));
//给新数组赋值
for (i = 0; i < n; i++)
{
arr1[arr[i] - min]++;
}
int j = 0;
//回收到原来的序列中
for (i = 0; i < sum; i++)
{
while (arr1[i]--)
{
arr[j++] = i + min;
}
}
}然后我们运行测试一下:
可以看到是有序的,选择排序就 OK 了;
3,计数排序的特性总结:
1, 计数排序在数据范围集中时,效率很高,但是适用范围及场景有限
2.,时间复杂度:O(N+K)
3, 空间复杂度:O(N)
4, 稳定性:稳定
二,排序算法复杂度及稳定性分析
| 排序方法 | 平均情况 | 最好情况 | 最坏情况 | 辅助空间 | 稳定性 |
| 冒泡排序 | O(N^2) | O(N) | O(N^2) | O(1) | 稳定 |
| 选择排序 | O(N^2) | O(N^2) | O(N^2) | O(1) | 不稳定 |
| 直接插入排序 | O(N^2) | O(N) | O(N^2) | O(1) | 稳定 |
| 希尔排序 | O(NlongN)~O(N^2) | O(N^1.3) | O(N^2) | O(1) | 不稳定 |
| 堆排序 | O(NlongN) | O(NlongN) | O(NlongN) | O(1) | 不稳定 |
| 归并排序 | O(NlongN) | O(NlongN) | O(NlongN) | O(N) | 稳定 |
| 快速排序 | O(NlongN) | O(NlongN) | O(N^2) | O(N) | 不稳定 |
| 计数排序 | O(N+K) | O(N+K) | O(N+K) | O(K) | 稳定 |
三,排序系列所有源代码
Sort.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include"Stack.h"
//打印
void PrintSort(int* arr, int n);
//插入排序
void InsertSort(int* arr, int n);
//希尔排序
void HillSort(int* arr, int n);
//选择排序
void SeleSort(int* arr, int n);
//堆排序
void HeapSort(int* arr, int n);
//向下调整
void DownAdjust(int* arr, int n, int i);
冒泡排序
//void BubblSort(int* arr, int n);
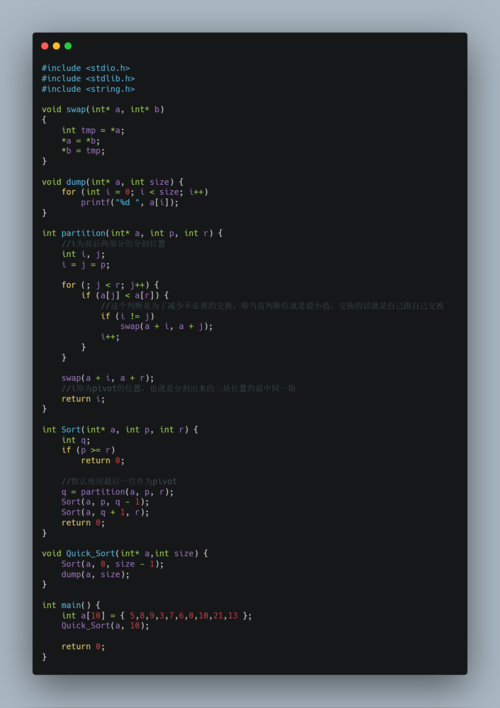
//快速排序
void QuickSort(int* arr, int begin, int end);
//三数取中
int middle(int* arr, int left, int right);
//快慢指针法
int PartSort3(int* arr, int left, int right);
//挖坑法
int PartSort2(int* arr, int left, int right);
//霍尔排序
int PartSort1(int* arr, int left, int right);
//快速排序(非递归)
void QuickNon(int* arr, int begin, int end);
//归并排序
void MergerSort(int* arr, int begin, int end);
//归并排序(非递归)
void MergerSortNon(int* arr, int begin, int end);
// 计数排序
void CountSort(int* arr, int n);
Sort.c
#define _CRT_SECURE_NO_WARNINGS 1
#include"Sort.h"
//打印
void PrintSort(int* arr, int n)
{
int i = 0;
for (i = 0; i < n; i++)
{
printf("%d ", arr[i]);
}
}
//交换
void Swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
//插入排序
void InsertSort(int* arr, int n)
{
int i = 0;
for (i = 0; i < n-1; i++)
{
int end = i;
int tmp = arr[end + 1];
while (end >= 0)
{
if (arr[end] >= tmp)
{
//交换
Swap(&arr[end], &arr[end+1]);
end--;
}
else
{
break;
}
}
arr[end + 1] = tmp;
}
}
//希尔排序
void HillSort(int* arr, int n)
{
int gap = n;
int i = 0;
while (gap > 1)
{
gap = gap / 2;
for (i = 0; i < n-gap; i++)
{
int end = i;
int tmp = arr[end + gap];
while (end >= 0)
{
if (arr[end] >= tmp)
{
//交换
Swap(&arr[end], &arr[end + gap]);
end -= gap;
}
else
{
break;
}
}
arr[end + gap] = tmp;
}
}
}
//选择排序
void SeleSort(int* arr, int n)
{
int begin = 0, end = n - 1;
while (begin < end)
{
int maxi = begin, mini = begin;
for (int i = begin; i <= end; i++)
{
if (arr[i] > arr[maxi])
{
maxi = i;
}
if (arr[i] < arr[mini])
{
mini = i;
}
}
Swap(&arr[begin], &arr[mini]);
// 如果maxi和begin重叠,修正一下即可
if (begin == maxi)
{
maxi = mini;
}
Swap(&arr[end], &arr[maxi]);
++begin;
--end;
}
}
//向下调整
void DownAdjust(int* arr, int n, int i)
{
int perent = i;
int child = perent* 2 + 1;
while (child<n)
{
if (child+1<n && arr[child + 1] > arr[child])
{
child++;
}
if (arr[perent] < arr[child])
{
//交换
Swap(&arr[perent], &arr[child]);
perent = child;
child = perent * 2 + 1;
}
else
{
break;
}
}
}
//堆排序
void HeapSort(int* arr, int n)
{
//建堆
int i = 0;
for (i = (n - 1 - 1) / 2; i >= 0; i--)
{
//向下调整
DownAdjust(arr, n, i);
}
//交换,删除排序法
while (n > 1)
{
//交换
Swap(&arr[0], &arr[n - 1]);
n--;
//向下调整
DownAdjust(arr, n, 0);
}
}
//三数取中
int middle(int* arr, int left, int right)
{
//int mid = (left +right)/ 2;
//随机数取中
int mid = left + (rand() % (right - left));
if (arr[left] < arr[mid])
{
if (arr[mid] < arr[right])
{
return mid;
}
if (arr[left] < arr[right])
{
return right;
}
else
{
return left;
}
}
//arr[mid]<=arr[left]
else
{
if (arr[mid] > arr[right])
{
return mid;
}
if (arr[left] > arr[right])
{
return right;
}
else
{
return left;
}
}
}
//霍尔排序
int PartSort1(int* arr, int left, int right)
{
//三数取中
int ret = middle(arr, left, right);
Swap(&arr[left], &arr[ret]);
int keyi = left;
while (left < right)
{
//右边先走
while (left<right && arr[right]>=arr[keyi])
{
right--;
}
//左边后走
while (left < right && arr[left] <= arr[keyi])
{
left++;
}
//交换
Swap(&arr[left], &arr[right]);
}
Swap(&arr[left], &arr[keyi]);
return left;
}
//挖坑法
int PartSort2(int* arr, int left, int right)
{
//三数取中
int ret = middle(arr, left, right);
Swap(&arr[left], &arr[ret]);
int key = arr[left];
int hole = left;
while (left < right)
{
while (left < right && arr[right] >= key)
{
right--;
}
arr[hole] = arr[right];
hole = right;
while (left < right && arr[left] <= key)
{
left++;
}
arr[hole] = arr[left];
hole = left;
}
arr[hole] = key;
return hole;
}
//前后指针法
int PartSort3(int* arr, int left, int right)
{
//三数取中
int ret = middle(arr, left, right);
Swap(&arr[left], &arr[ret]);
int keyi = left;
int slow = left, fast = left+1;
while (fast<=right)
{
if (arr[fast] < arr[keyi] && ++slow!=fast)
{
//交换
Swap(&arr[fast], &arr[slow]);
}
fast++;
}
Swap(&arr[slow], &arr[keyi]);
return slow;
}
//插入排序(改造版)
void InsertSort1(int* arr, int left, int right)
{
int i = 0;
for (i = left; i < right; i++)
{
int end = i;
int tmp = arr[end + 1];
while (end >= 0)
{
if (arr[end] >= tmp)
{
//交换
Swap(&arr[end], &arr[end + 1]);
end--;
}
else
{
break;
}
}
arr[end + 1] = tmp;
}
}
//快速排序
void QuickSort(int* arr, int begin, int end)
{
srand(time(0));
if (begin >= end)
{
return NULL;
}
if (end - begin <10)
{
InsertSort1(arr,begin,end);
}
else
{
int keyi = PartSort1(arr, begin, end);
//排序[begin,keyi) & [keyi+1,end]
QuickSort(arr, begin, keyi);
QuickSort(arr, keyi + 1, end);
}
}
//快速排序(非递归)
void QuickNon(int* arr, int begin, int end)
{
srand(time(0));
ST ps;
//初始化
STInit(&ps);
if (begin >= end)
{
return;
}
//插入
STPush(&ps, end);
STPush(&ps, begin);
//栈不为空就进去
while (!STEmpty(&ps))
{
int left = STInsert(&ps);//栈顶元素
STPop(&ps);//删除
int right = STInsert(&ps);
STPop(&ps);
int keyi = PartSort1(arr, left, right);
//排序[left,keyi-1] & [keyi+1,right]
if (keyi + 1 < right)
{
//插入
STPush(&ps, right);
STPush(&ps, keyi + 1);
}
if (left < keyi - 1)
{
//插入
STPush(&ps, keyi - 1);
STPush(&ps, left);
}
}
//销毁
STDestroy(&ps);
}
//归并
void Merger(int* arr, int* tmp,int begin,int end)
{
int mid = (begin + end) / 2;
if (begin == end)
{
return;
}
//排序【begin,mid】& 【mid+1,end】
Merger(arr, tmp, begin,mid);
Merger(arr, tmp, mid+1, end);
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = 0;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
{
tmp[i++] = arr[begin1++];
}
else
{
tmp[i++] = arr[begin2++];
}
}
while(begin1 <= end1)
{
tmp[i++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = arr[begin2++];
}
//进行拷贝
memcpy(arr + begin, tmp, (end - begin+1)*sizeof(int));
}
//归并排序
void MergerSort(int* arr, int begin, int end)
{
if (begin >= end)
{
return;
}
//开辟同等大小数组
int* tmp = (int*)malloc((end - begin + 1)*sizeof(int));
//归并
Merger(arr, tmp, begin, end);
free(tmp);
tmp = NULL;
}
//归并排序(非递归)
void MergerSortNon(int* arr, int begin, int end)
{
if (begin >= end)
{
return;
}
//开辟同等大小数组
int* tmp = (int*)malloc((end - begin + 1) * sizeof(int));
int gap = 1;
int j = 0;
while (gap < end)
{
for (j = 0; j < end; j += 2 * gap)
{
int begin1 = j, end1 = begin1+gap-1;
int begin2 =end1+1, end2 = begin2+gap-1;
int i = 0;
//处理边界问题
if (end1 >= end)
{
break;
}
if (end2 >end)
{
end2 = end;
}
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
{
tmp[i++] = arr[begin1++];
}
else
{
tmp[i++] = arr[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = arr[begin2++];
}
//进行拷贝
memcpy(arr + j, tmp, (end2 - j+ 1) * sizeof(int));
}
gap *= 2;
}
free(tmp);
tmp = NULL;
}
// 计数排序
void CountSort(int* arr, int n)
{
int i = 0;
int max = arr[0], min = arr[0];
//找最大,最小值
for (i = 0; i < n; i++)
{
if (arr[i] > max)
{
max = arr[i];
}
if (arr[i] < min)
{
min = arr[i];
}
}
//空间大小
int sum = max - min + 1;
//开辟空间并且使元素值都为0
int* arr1 = (int*)calloc(sum, sizeof(int));
//给新数组赋值
for (i = 0; i < n; i++)
{
arr1[arr[i] - min]++;
}
int j = 0;
//回收到原来的序列中
for (i = 0; i < sum; i++)
{
while (arr1[i]--)
{
arr[j++] = i + min;
}
}
}Stack.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef int STDataType;
typedef struct StackTop
{
STDataType* a;
int top;
int capacity;
}ST;
//初始化
void STInit(ST* ps);
//销毁
void STDestroy(ST* ps);
//插入
void STPush(ST* ps, STDataType x);
//删除
void STPop(ST* ps);
//返回栈顶
STDataType STInsert(ST* ps);
//数量
int STSize(ST* ps);
//判断是否为空
int STEmpty(ST* ps);
Stack.c
#define _CRT_SECURE_NO_WARNINGS 1
#include"Stack.h"
//初始化
void STInit(ST* ps)
{
assert(ps);
ps->a = NULL;
ps->top = ps->capacity = 0;
}
//销毁
void STDestroy(ST* ps)
{
assert(ps);
free(ps->a);
ps->a = NULL;
ps->top = ps->capacity = 0;
}
//插入
void STPush(ST* ps, STDataType x)
{
assert(ps);
if (ps->top == ps->capacity)
{
ps->capacity = ps->top == 0 ? 4 : ps->capacity*2;
ps->a = (STDataType*)realloc(ps->a,sizeof(STDataType)*ps->capacity);
}
ps->a[ps->top] = x;
ps->top++;
}
//删除
void STPop(ST* ps)
{
assert(ps);
assert(ps->top > 0);
ps->top--;
}
//返回栈顶
STDataType STInsert(ST* ps)
{
assert(ps);
assert(ps->top > 0);
return ps->a[ps->top-1];
}
//数量
int STSize(ST* ps)
{
assert(ps);
return ps->top;
}
//判断是否为空
int STEmpty(ST* ps)
{
assert(ps);
if (ps->top == 0)
{
return 1;
}
else
{
return 0;
}
}同志们!排序的知识就到这里了!
后面博主会陆续更新;
如有不足之处欢迎来补充交流!
完结。。

