蓝桥杯C/c++
头文件
万能头文件:#include<bits/stdc++.h>
该头文件虽然减轻了记忆头文件的负担,但编译器每次编译翻译单元时都必须实际读取和分析每个包含的头文件,如不必要可以减少这类头文件的使用。
实用函数及运算符
求幂次
pow(x,y):表示以x为底的y次方。注意这里的x,y数据类型应为double型。
移位运算符
<<: x<<y==x*(2^y)
>>:x>>y==x/(2^y)
STL排序sort()函数
- void sort(first,last);
- void sort(first,last,***p);
复杂度为O(nlogn),排序的范围为[first,last),包括first不包括last。
例如要对数组a第二到九个元素从大到小排序,即sort(a+1,a+9,greater);
***p表示排序方法,自带4中排序方式:less、greater、less_equal、greater_equal。默认从小到大进行排序,即less。
也可以自定义排序方式,常用于结构体排序:
struct Student{
char name[256];
int score;//分数
}
bool cmp(struct Student* a,struct Student* b){
//按分数从小到大排序
return a->score>b->score;
}
...
vector<struct Student* >list;//定义list,把学生信息存到list里
...
sort(list.begin(),list.end(),cmp);
优点:能在原数组上排序,不需要新的空间;能在数组的局部区间上排序。
依次读取数据
本写法用于连续读入一组数据直到末尾,用于事先不知道要读入数据个数的情况。
注意:DevC++无法使用此写法,但考试oj可以通过。
int a[N];
int ***t=0;
while(scanf("%d",&a[***t])!=EOF) ***t++;
STL全排列函数next_permutation()
该函数用于求出下一个排列。例如对由三个字符{a,b,c}组成的序列,next_permutation()可以按字典序返回6种排列:abc、acb、bac、bca、cab、cba。有如下两种形式:
bool next_permutation(first,last);bool next_permutation(first,last,***p);
该函数排列范围[first,last),包括first,不包括last。
返回值:如果没有下一个排列组合,则返回false,否则返回true,每执行一次,新的排列放回到原来的空间(例如原来的字符串s会变成新的字符排列顺序)中。
该函数用于逐个输出更大的全排列,而不是所有排列。如果要得到所有的全排列,就需要从最小的全排列开始。如果初始的全排列不是最小的,需要先用sort()对全排列排序,得到最小的全排列后,再使用next_permutation(),例如:
string s="bca";
sort(s.begin(),s.end());//字符串内部排序,得到最小的排列"abc"
do{
cout<<s<<" ";
}while(next_permutation(s.begin(),s.end()));
//s.end()指向最后一个字符的下一个位置
C++中还有全排列函数prev_permutation(),用于求前一个排列。
求数组最大/最小值
max_element(first,last);
min_element(first,last);
返回容器中的最大、最小值。注意区间左闭右开,不包括last,在题目规模不大的情况下可用。
初始化函数memset()
memset()作用是将某一块内存中的全部设置为指定的值。
例如:memset(arr,0,sizeof(arr))
其中arr表示要填充的内存块(一维数组等),0表示将该内存块所有值初始化为0,sizeof(arr)表示填充字符数。
GCD(最大公约数)和LCM(最小公倍数)
-
GCD(最大公约数),即能同时整除a,b的最大整数,记为
gcd(a,b)。性质:
-
gcd(a,b)=gcd(a,a+b)=gcd(a,ka+b)
-
gcd(ka,kb)=kgcd(a,b)
-
若gcd(a,b)=d,则gcd(a/d,b/d)=1,即a/d与b/d互素。(重要)
C++库函数(__gcd):可能会返回负数。
cout<<__gcd(15,81)<<endl;//输出3
cout<<__gcd(0,44)<<endl;//输出44,0和其他数取其他数
cout<<__gcd(0,0)<<endl;//输出0
cout<<__gcd(-6,-15)<<endl;//输出-3
cout<<__gcd(-17,289)<<endl;//输出-17
cout<<__gcd(17,-289)<<endl;//输出17
自行编写GCD代码,功能和库函数完全一样,也可能输出负数,需要的时候可以把int改成long long。
int gcd(int a,int b){
return b?gcd(b,a%b):a;
}
-
LCM:a和b的最小公倍数lcm(a,b)=a/gcd(a,b)×b。
int lcm(int a,int b){ //需要的时候把int改成long long return a/gcd(a,b)*b; //先做除法再做乘法,防止溢出 }
C++字符串函数
-
find()函数:查找 -
substr()函数:查子串 -
replace()函数:替换string& replace(size_t pos, size_t n, const char *s); //将当前字符串从pos索引开始的n个字符,替换成字符串s string& replace(size_t pos, size_t n, size_t n1, char c); //将当前字符串从pos索引开始的n个字符,替换成n1个字符c string& replace(iterator i1, iterator i2, const char* s); //将当前字符串[i1,i2)区间中的字符串替换为字符串s -
insert()函数:插入或push_back()函数:字符串尾部插入字符
-
append()函数:添加字符串str.append("***");在字符串str后面添加字符串 -
swap()函数:交换字符串 -
***pare()函数:比较字符串s1.***pare(s2)也可以直接比较:
if(s1==s2)return true; -
tolower()和toupper()函数:字符串转大小写#include <iostream> #include <string> using namespace std; int main() { string s = "ABCDEFG"; for( int i = 0; i < s.size(); i++ ) { s[i] = tolower(s[i]); } cout<<s<<endl; return 0; }
实用数据结构模板
vector
vector意为向量,它是STL的动态数组,可以在运行中根据需要改变数组的大小。
vector的头文件为#include<vector>
创建vector<int>a,vector与数组基本一致。
在加入元素时用到push_back()函数,即a.push_back(1);
数组大小用size()表示,即a.size(),该大小会随元素个数增多而自动变大。
链表list
STL list是双向链表,通过指针访问结点数据,它的内存空间可以是不连续的,使用它能高效地删除和插入结点。
//定义一个list
list<int>node;
//为链表赋值,例如定义一个包含n个结点的链表
for(int i=1;i<=n;i++)
node.push_back(i);
//遍历链表,用it遍历链表,例如从头遍历到尾
list<int>::iterator it =node.begin();
while(node.size()>1){
//list的大小由STL管理
it++;
if(it==node.end())//循环链表,end()是list末端下一位置
it=node.begin();
}
//删除一个结点
list<int>::iterator next=++it;
if(next==node.end())next=node.begin();//循环链表
node.erase(--it); //删除这个结点,使得node.size()自动减1
it=next; //更新it
队列
使用C++的STL queue,不用自己管理队列,代码很简洁。
-
queue<Type> q:定义队列,Type为数据类型,如int,float,char等。 -
q.push(item):把item放进队列。 -
q.front():返回队首元素,但不进行删除。 -
q.pop():删除队首元素。 -
q.back():返回队尾元素。 -
q.size():返回元素个数。 -
q.empty():检查队列是否为空。
C++优先队列
优先队列的特点是最优数据始终位于队首。优先队列效率很高:新数据插入队列生成新队首元素,复杂度O(logn),弹出最优队首元素在队列中计算新最优队首元素,复杂度O(logn)。
C++STL优先队列priority_queue用堆来实现。
定义:priority_queue<Type,Container,Functional>
Type是数据类型,Container是容器类型(用数组实现的容器,默认vector),Functional是比较的方式。当使用自定义数据类型时才需要传入这3个参数,而使用基本数据类型时,只需传入数据类型。如priority_queue<int>pq; 默认是大顶堆,堆顶是最大值。 部分操作如下:
-
priority_queue<Type,Container,Functional> pq:定义队列 -
pq.push():入队 -
pq.pop():出队 -
pq.size():返回当前队列元素个数 -
pq.top():返回队首元素 -
pq.empty():判断是否为空(空返回1,非空返回0)
栈(stack)
栈的特点是先进后出。在常用的递归中,系统中是用栈来保存“现场”的。
STL stack的有关操作如下。
-
stack<Type> s:定义栈,Type为数据类型,如int、float、char等。 -
s.push(item):把item放到栈顶。 -
s.top():返回栈顶元素,但不将其删除。 -
s.pop():删除栈顶元素,但不会返回。出栈需要进行两步操作:先获取栈顶元素,再删除栈顶元素。 -
s.size():返回栈中元素个数。 -
s.empty():检查栈是否为空,如果为空返回true,否则返回false。
集合(set)
set是集合,用来对一组元素进行查重去重(集合内不会有重复元素)
-
insert():插入 -
size():元素个数 -
erase():删除某个元素 -
clear():清空集合元素 -
empty():判断集合是否为空 -
find():查找指定元素 -
upper_bound(起始地址,结束地址,要查找数值):二分查找,返回第一个大于待查找数值出现的位置。
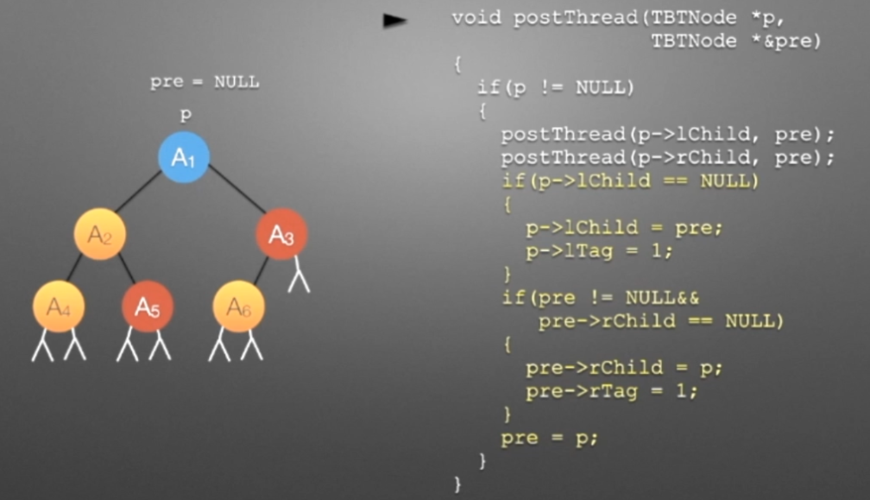
二叉树存储
二叉树的一个结点,需要存储结点的值,以及指向左右子节点的指针。
在算法竞赛中,为了使代码简洁高效,一般用静态数组实现二叉树。定义一个大小为N的静态结构体数组,用它来存储一棵二叉树:
struct Node{ //静态二叉树
char value;
int lson,rson; //指向左右子节点的存储位置,编程时可简写为ls或l
}tree[N]; //编程时可简写为t
满二叉树tree[N]的空间需要设为N=4m,即元素数量的4倍。
实用算法模板
按字典序排序
有些情况下排序是按照字典序排序,也就是把数字看作字符串来排序,如排序"7,13"按字典序排序,应该输出"713"而不是"137"。
bool cmp(string a,string b){ //从大到小,按字典序的反序排列
return a+b>b+a; //组合字符串
}
素数判断
当n≤10^14时,用试除法判断。复杂度O(n½)
用[2,n½]内的所有数去试着除n,如果都不能整除,n就是素数。因为如果n有个因子小于n½,就不用再试。
bool is_prime(long long n){
if(n<=1) return false; //1不是素数
for(long long i=2;i<=sqrt(n);i++)
if(n%i==0)return false;//能整除,不是素数
return true;
}
快速幂
采用倍增原理。
int fastPow(int a,int n){//计算aⁿ
int ans=1; //用ans返回结果
while(n){ //把n看成二进制数,逐个处理它最后一位
if(n&1) ans*=a; //&按位与操作,如果n的最后一位是1,表示这个地方需要参与计算
a*=a; //递推:2次方--4次方--八次方···
n>>=1; //n右移一位,把刚处理过的n的最后一位去掉
}
return ans;
}
幂运算的结果往往很大,一般题目会要求先取模再输出。根据取模的性质有:aⁿ mod m=(a mod m)ⁿ mod m。
给快速幂函数加上取模操作:
typedef long long ll;
ll fastPow(ll a, ll n,ll mod){
ll ans=1;
a%=mod; //重要,防止下面的ans*a越界
while(n){
if(n & 1) ans=(ans*a)%mod; //取模
a=a*a%mod; //取模
n>>=1;
}
return ans;
}
矩阵乘法和快速幂
两个矩阵A和B相乘,要求A的列数等于B的行数,设A是m×n的矩阵,B是n×u的矩阵,那么乘积C=AB是m×u的矩阵,三重循环,复杂度为O(mnu)。
矩阵的幂可以用快速幂来计算,从而极大地提高效率,复杂度O(N³logn),其中N³对应矩阵乘法,logn对应快速幂。出题时一般会给一个小N(方阵行列数)和一个较大的n(幂次),来考察快速幂的运用。
struct matrix{int m[N][N];}; //定义矩阵,常数N是矩阵的行数和列数
matrix operator * (const matrix& a,const matrix& b){
//重载*为矩阵乘法,注意const
matrix c;
memset(c.m,0,sizeof(c.m)); //清零
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
for(int k=0;k<N;k++)
c.m[i][j]+=a.m[i][k]*b.m[k][j]; //不取模
//c.m[i][j]=(c.m[i][j]+a.m[i][k]*b.m[k][j])%mod; //取模
return c;
}
matrix pow_matrix(matrix a,int n){//矩阵快速幂,和普通快速幂几乎一样
matrix ans;
memset(ans.m,0,sizeof(ans.m));
for(int i=0;i<N;i++)ans.m[i][i]=1;//初始化为单位矩阵,类似普通快速幂的ans=1
while(n){
if(n&1)ans=ans*a; //不能简写为ans*=a,因为*重载了
a=a*a;
n>>=1;
}
return ans;
}
尺取法
又称双指针,指在区间操作时,用两个指针同时遍历区间,从而实现高效率操作。简单来说,就是把两重循环转化为一重循环。复杂度从O(n²)变为O(n)。如:
for(int i=0;i<n;i++) //i从头扫描到尾
for(int j=n-1;j>=0;j--) //j从尾扫描到头
{...}
//尺取法
for(int i=0,j=n-1;i<j;i++,j--)
{...}
应用限制:要求i<j
二分法
二分法概念很简单,每次把搜索范围缩小为上一次的1/2,直到找到答案为止。
整数二分
整数二分易理解不易编程,由于整数的取整问题,容易出错。应用场景:存在一个有序的数列;能够把题目建模为在有序数列上查找一个合适的数值。
下面例子是在一个区间1-N内找到符合条件的最大数值。
int L=1,R=N;
//第一种写法
while(L<R){
int mid=(L+R+1)/2; //除以2,向右取整
if(check(mid)) L=mid; //新的搜索区间是右半部分,R不变,调整L=mid
else R=mid-1; //新的搜索区间是左半部分,L不变,调整R=mid-1
}
cout<<L;
//第二种写法
while(L<R){
int mid=(L+R)/2; //除以2,向左取整
if(check(mid)) L=mid+1; //新的搜索区间是右半部分,R不变,更新L=mid+1
else R=mid; //新的搜索区间是左半部分,L不变,更新R=mid
}
cout<<L-1;
实数二分
实数二分不用考虑整数取整问题,较容易。可以用来求解方程的根。
const double eps=1e-7; //精度,如果用for循环,可以不要eps
while(right-left>eps){ //for(int i=0;i<100;i++)
double mid=left+(right-left)/2;
if(check(mid))right=mid; //判定,然后继续二分
else left=mid;
}
前缀和
一个长度为n的数组a[0]~a[n-1],它的前缀和sum[i]等于a[0]到a[i]的和。
利用递推,只需n次就能计算出所有的前缀和: sum[i]=sum[i-1]+a[i]。
也能用sum[]反推计算a[]:a[i]=sum[i]-sum[i-1]
快速计算出数组任意一个区间a[i]~a[j]的值:sum[j]-sum[i-1]
应用:
//例:当n=4时,ans=a1*a2+a1*a3+a1*a4+a2*a3+a2*a4+a3*a4 =a1*(a2+a3+a4)+a2*(a3+a4)+a3*a4
#include <iostream>
using namespace std;
int main()
{
unsigned long long S=0;
int n;
cin>>n;
int *a=new int[n];
for(int i=0;i<n;i++)cin>>a[]
unsigned long long *sum=new unsigned long long[n-1];//利用前缀和求解
sum[0]=a[0];
for(int i=1;i<n-1;i++){
sum[i]=sum[i-1]+a[i];
}
for(int i=1;i<n;i++){
S+=sum[i-1]*a[i];
}
cout<<S;
return 0;
}
搜索(DFS和BFS)
具体介绍可参考:DFS和BFS
应用场景:
- DFS:查找所有路径(排列组合、正则问题、输出迷宫所有路径)
- BFS:找出最短路径
计算机工具
Excel使用
求和
例题如下:
在Excel表格的B列填分母,每行是前一行的两倍,在B2单元格填写“=B1*2”,然后将鼠标指针移动到B2单元格的右下角,当指针变成十字形状时,按住鼠标左键向下拖拽到第20行,就填好了分母。
最后通分求和。分母就是B20单元格中的524288,分子的计算公式实际上就是“SUM(B1:B20)"。只要选中B1到B20区域,Excel自动计算出结果1048575。
日期问题
算法题中有许多问题涉及到求两个日期之间的天数差,具体方法如下:
选中单元格在公式—日期和时间中选择“DATE”,填写日期。
利用公式计算结果。
Windows自带计算器
考试时可以采用Windows自带的计算器来解决一些数学问题。
例如在求1000!时,打开计算器,选择“科学”模式,输入要求阶乘的数字1000,再点击n!即可得到结果。

